Modern Portfolio Theory
April 2, 2025
What is Modern Portfolio Theory (MPT)?
Modern Portfolio Theory (MPT), developed by economist Harry Markowitz in 1952, is a fundamental investment strategy that helps investors optimize their portfolios by balancing risk and return. This theory provides a quantitative framework for making investment decisions by selecting the optimal mix of assets to maximize expected returns while minimizing risk.
MPT is based on the principle that investors can diversify their portfolios to reduce overall risk. By allocating assets strategically, investors can achieve an efficient portfolio, where returns are maximized for a given level of risk. The theory relies solely on risk and return analysis, making it a cornerstone of modern investment strategies.
How Modern Portfolio Theory Works
The key idea behind MPT is the risk-return tradeoff. Investors with higher risk tolerance may allocate more capital to high-risk, high-return assets, while conservative investors may prefer lower-risk portfolios. The theory also introduces the concept of the efficient frontier, which represents the optimal set of portfolios offering the highest return for a given level of risk.
Why is Modern Portfolio Theory Still Relevant?
Although many new investment models have evolved since MPT’s introduction, its core principles remain highly relevant in today’s financial markets. Investment professionals, asset managers, and financial analysts continue to use MPT as a foundation for portfolio construction and risk management.
Key Learning Points
- Modern Portfolio Theory assumes that all investors are rational
- Investors can vary the portfolio weighting in various assets or asset classes, in order to determine optimal portfolios
- MPT analysis results in what is termed the “Efficient Frontier”
- The MPT is considered too simplistic by many and further theories have been built upon it
Modern Portfolio Theory Key Assumptions
MPT takes into account many assumptions that are not always realistic or correct in the real world. It still stands as a basis for portfolio asset allocation. While the theory has been challenged, mainly due to the various assumptions, it remains one of the best-known and widely used.
The key MPT assumptions are:
- Returns are distributed along a normal “bell curve”.
- Correlations do not change over time.
- Investors will make rational investment decisions and will avoid unnecessary risk.
- Asset volatility is known and constant.
- No taxes or transaction costs.
Types of MPT Strategies
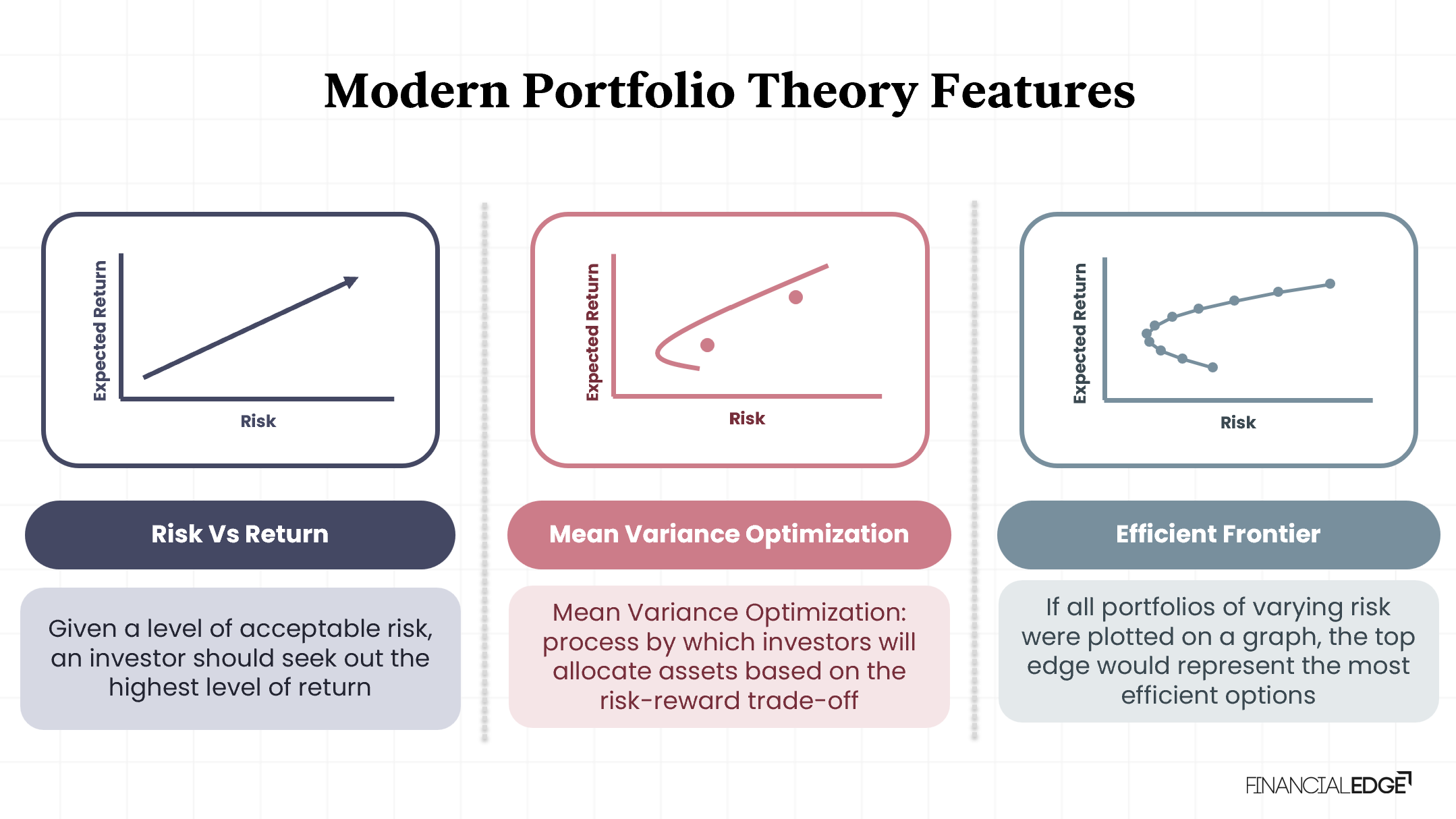
Modern Portfolio Theory (MPT) involves several strategies, including:
- Risk vs. Return forms a key feature of the theory. Investors should seek the highest return for an acceptable level of risk.
- Mean Variance Optimization (MVO) identifies the portfolio weights that will deliver the highest return while considering risk budgets.
- Efficient Frontier involves plotting portfolios to find the ones that offer the highest expected return for a given level of risk.
Risk vs. Return
All investors are risk averse. It’s one of the strongest assumptions in MPT, even though it is not present in the real world. An investor will take on increased risk only if compensated by higher expected returns. Conversely, an investor who wants higher expected returns must accept more risk. Different investors will evaluate the trade-off differently based on individual risk aversion characteristics or risk tolerance. For example, retirees typically choose lower risk routes compared to younger professionals.
Mean Variance Optimization
The MPT assumes that all investors are rational i.e. given an acceptable level of risk, all investors attempt to achieve the highest level of return for that level of risk. Additionally, investors who are wanting a particular targeted level of return should seek out the lowest level of risk for that return level. This can be done by Mean-Variance Optimization (MVO).
The MVO is the process by which investors will allocate portfolios based on the risk-reward trade-off. This is done by investors varying the weightings in various assets or asset classes to determine which portfolios provide the best risk-return trade-off. Such analysis results in what is termed as the “Efficient Frontier”.
The Efficient Frontier is created graphically – if all portfolios of varying risks are plotted on a graph against the expected return for those portfolios. The top edge of the graph would represent the most efficient portfolio.
The Efficient Frontier
This is the set of efficient or optimal portfolios that an investor can choose from. Such portfolios offer the highest expected return for a defined level of standard deviation (risk), or the lowest standard deviation for a given level of expected return. Portfolios that lie below this frontier are not efficient or optimal, as they do not provide adequate returns commensurate to the level of risk.
Suppose we chart four portfolios A, B, C, and D against their respective expected return (Y-axis) and risk (i.e. standard deviation, X-axis). Now, if portfolio A and C have the same level of risk (i.e. standard deviation) but portfolio A produces a lower expected return, then this portfolio is inferior to portfolio C. Furthermore if we compare portfolios B and D, and both have the same expected return but portfolio B has a higher standard deviation (risk), then portfolio D is superior to portfolio B i.e. portfolio D is more optimal and efficient.
When we chart the outermost portfolios, we would plot the efficient frontier. Every investor in theory should only seek portfolios on the efficient frontier line.
No investor would likely choose to invest in a portfolio that is to the right of the efficient frontier as the portfolio on the frontier can offer the same return for a lower level of risk. Finally, where exactly would an investor choose to allocate on the efficient frontier, is determined by each investor’s risk tolerance and return objectives?
Having stated the above, the MPT is considered too simplistic by many, as it considers only two factors – risk and returns in analysis, rather than multiple factors. Further, the MPT is typically backward-looking.
Modern Portfolio Theory – Example
For example, Given below are portfolios A, B, C, and D. Each portfolio is made up of four assets. The individual expected return on these assets, along with their respective weightings in each of the four portfolios (A, B, C, and D), is also stated. Further, the standard deviation (risk) of each portfolio is given. Thereafter, the expected return on portfolios A, B, C, and D has been calculated below.




After calculating the expected return on each portfolio (A, B, C, and D) and taking into account their respective standard deviation, we can infer that both portfolios C and D are inefficient. This is because other portfolios can attain a higher expected rate of return with lower risk.
Pros and Cons of MPT
Pros
- Modern Portfolio Theory helps investors manage risk by diversifying their portfolios.
- Modern Portfolio Theory allows investors to maximize their expected return for a given level of risk.
Cons
While Modern Portfolio Theory is very influential, it is important to be aware of the criticisms:
- Modern Portfolio Theory is too simple. More complex models have been created adding more factors other than risk and return.
- Backward looking analysis can have low predictive value for the future.
- Not all investors act rationally but Modern Portfolio Theory assumes they do.
- Not all investors have the ability to invest in risky assets alone and the markets aren’t always efficient.
Modern Portfolio Theory Vs CAPM
Modern Portfolio Theory focuses on the trade-off between risk and return, using diversification to optimize portfolios. CAPM (Capital Asset Pricing Model) explains the relationship between expected return and market risk, considering both systematic and unsystematic risks. While Modern Portfolio Theory emphasizes portfolio optimization, CAPM provides a framework for pricing individual assets based on their risk relative to the market.
Conclusion
Modern Portfolio Theory (MPT) remains a cornerstone in the field of investment management. Despite its simplicity and the criticisms it faces, MPT provides a valuable framework for understanding the trade-off between risk and return. By focusing on diversification and optimizing portfolios, investors can achieve the highest possible returns for a given level of risk. While newer models and theories have built upon MPT, its principles continue to be relevant in today’s investment world. Understanding and applying MPT can help investors make informed decisions and navigate the complexities of portfolio management.